#25 - Composites in Plain English Pt. 3

This post will explore why we don’t just knit airplanes out of yarn. In part 1 of my exploration of fiber-based composites, I learned why fibers are so strong, and then, in part 2, how those wispy fibers can be brought together into more usable yarns or tows. Two whole parts on just the fibers. Of course, this series is not about fibers, but about composites. It’s time to introduce the second character in our story: glue.
The glue in a composite goes by many names. Engineering textbooks call it a “matrix” -- maybe because fibers are stuck in the Matrix. It’s also called “epoxy”, “resin”, “plastic”, “polymer”, etc., etc. Some terms are generic while some are specific to certain materials. That gets way too confusing, so I’m just going to stick to calling it glue. But what really is glue? This is a deceptively simple question. For my favorite explanation, I’ll turn to J.E. Gordon’s The New Science of Strong Materials:
Any two solids can therefore be glued together if we can find a liquid which will wet them both and then harden... Wood can be glued very well by wetting it with water which is subsequently frozen.
In the composites we’re discussing here, the two solids being glued together are fibers and more fibers. That is the basic building block of fiber-based composites: fibers glued to each other.
When we last left our fibers, we had bundled them into tow and twisted them into yarn -- both of which (tow and yarn) I’ll just generically call “strands”. To understand the role of glue in a composite, we’ll compare a strand that is glued with a strand that isn’t.
(Those of you who were really paying attention in part two might be saying “Hold on just a minute. I thought tow was a bunch of fibers that were already glued together. How can you add glue to something that’s already been glued?” The answer is that the glue in tow is extremely minimal -- just barely enough to keep things together. Think of tow as a good pulled pork, falling apart at the slightest touch. For our purposes, we can ignore that small amount of glue. I can assure you that if you play around with a tow, it feels no different than a yarn.)
This first thing we’ll consider is a strand under compression. All that means is that we’re grabbing the ends of the strand and pushing them closer together. An unglued strand acts no differently than a piece of string -- the two ends come together without any resistance, and the strand hangs floppily below. No surprises there. But what does this mean about the strand? Does it not have any strength when it comes to compression? Not exactly. What it lacks is stability.
This is compression’s game: for the most part, strength is not the limiting factor, stability is. Stand a sheet of paper straight up on your desk, holding it near the bottom. It’s not even able to support its own weight, slumping over sadly. Now roll up the paper into a tube. Not only can it support its own weight, it can also support the weight of something pretty substantial, like a book. In both cases, the material is the same -- even the amount of material is the same, it’s just been arranged in a more stable way.
So we know that our unglued strand lacks stability and flops out of the way when we push on it. What happens when we add glue? When you push on a glued strand, it feels stiff. It’s like an uncooked spaghetto -- compared to an unglued strand, which feels like a cooked spaghetto. The glue somehow adds stability to the strand. But how? The glued and unglued strands don’t look any different to each other, and we definitely haven’t manipulated the shape of the strand like we did with the sheet of paper.
It turns out that while the outside of the strand hasn’t changed at all, the inside has. Remember that our strand -- tow or yarn -- is made up of thousands of individual fibers. When we add glue, we bind the fibers in the strand together. Imagine grabbing a big handful of pens, standing them up on a table, and then letting go. The pens fall over. Now imagine tying all those pens together with a rubber band around the outside. This bundle of pens can stand on its own. The pens represent the fibers and the rubber band represents the glue. What you get when you rubber band a bunch of pens together or add glue to a strand is basically one thick column instead of a thousand thin columns. This is the key behind the increased stability.
Is a thick column really that much more stable than a thin column? Well, yes. You’ve experienced this yourself, though not in column form. Take PET, a type of plastic: in thick form, it’s the plastic bottle that contains and protects your Dr. Pepper; in thin form, it’s the fibers which make up the polyester fabric in your workout shirt. It’s the same material in both cases but its thickness or thinness makes a huge difference in how it acts under compression. It’s the same with glass: in a thick rod or pane, it can resist compression; in a thin fiber, it behaves just like an ordinary string.
So thickness has a big effect on stability. How big? For the answer to that, I’ll turn to equations (dun dun dunnnn). I try to avoid equations as much as possible -- food analogies are much more fun -- but they can be illustrative. I’ll be using Euler’s formula for column buckling. “Column” here just refers to a long, thin structure (like our fibers), and “buckling” to the instability we’ve already discussed. So this equation attempts to predict when a column will buckle. I’m going to model the glued strand as one thick column and the unglued strand as a thousand thin columns. For simplicity, I’ll assume that everything besides the thickness (i.e., material, length, etc) are the same in both the thick and thin columns. That assumption will allow me to focus in on just the relationship between thickness and stability.
The equations I’m using are here and here if you want more detail. The radius of the thin column is the radius of a single glass or carbon fiber. The radius of the thick column is that of the smallest circle that one thousand fibers can be packed into,calculated using this tool. (I input the fiber diameter for the smaller circle and adjust the large diameter until the number was roughly 1000. Happens to 1094 fibers in this case.)

After all that, we find that the thick cylinder (the strand) is about 2 million times more capable than the thin cylinder (the fiber). In other words, a glued strand is 2,000 times more capable in compression than an unglued strand, which is made of a thousand fibers.
The big takeaway here is that glue makes a composite more capable in compression by allowing the fibers to work together, not by being strong in compression itself. Don’t believe me? Let’s do a little thought experiment and see what happens if we can get the fibers to work together without using glue at all. If that matches the capability of the glued strand, we’re in business.
Imagine that we take an unglued strand and put a magical rubber band around the outside. The magic band ties our fiber bundle together so tightly that it squeezes out all of the little air pockets between the fibers, essentially turning it into a single column. But wait, I already modeled the glued strand as a single column. What’s the difference? The difference is that glue filled up those air pockets in the glued strand, whereas here, we’ve just squeezed them out completely, leaving us with a thinner column.
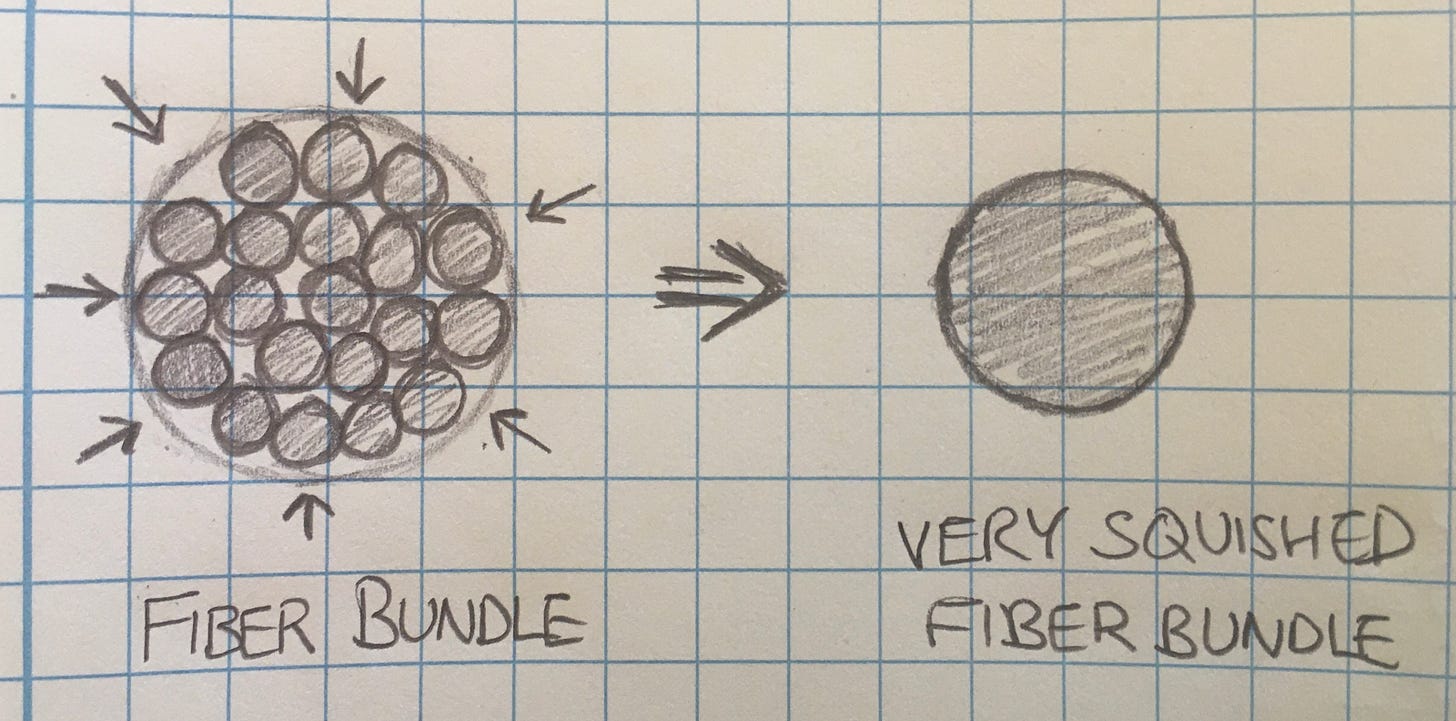
Let’s see how this one, which I’ll called the squished column, compares to our original glued strand, the thick column.
The squished radius was calculated by finding the total cross sectional area of the fibers used in the previous calculation. 1094 fibers at a radius of .0002”.

The glued strand is only ~1.7 times more capable under compression than our magic band strand. That’s not very significant at all. Our idea about the role of glue seems reasonable.
Did I cheat by transforming the fibers into a single column? Not really. In an unglued strand, the air pockets are distributed evenly throughout the cross section. That’s tricky to calculate, so I chose to simplify the problem. There are two options for simplification: (1) Push the air out, leaving a thinner column (2) Pull the air in, resulting in a column as thick as it was before but with a hole down the center. The truth is somewhere in the middle. I made a conservative assumption by picking the worst case.
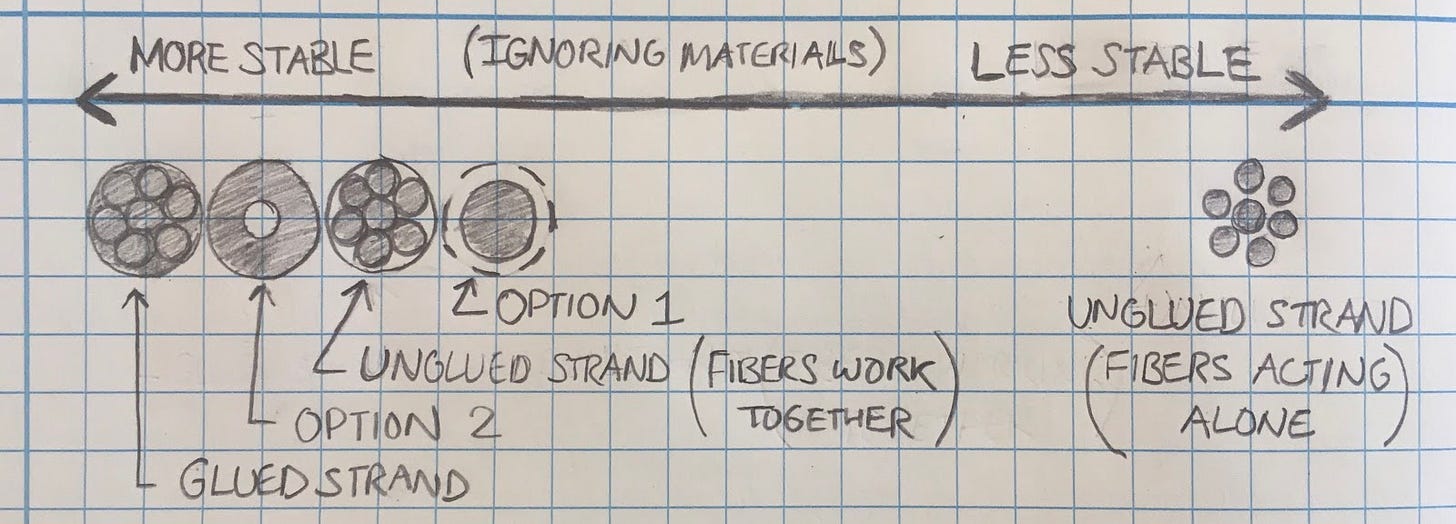
Why is Option 1 the worst case scenario? Because a hollow cylinder is a better use of material than a solid cylinder, in compression. You can see this in the equations from before. The radius term tells us that the farther the material is away from the middle, the more effective it is. That’s why the rolled up paper outperforms the sheet that you stood up on your table. The tube has material uniformly far away from the center. The sheet has a lot of material far from the center along its width, so it’s sturdy in that direction; but along its thickness, there’s hardly any material farther than a hairsbreadth away. That’s why the paper always flops over in that thinnest direction. All that to say: even with our conservative assumption, a strand held together with magic is about as capable as a strand held together with glue. The glue’s strength is not important. Its ability to tie the strands together is.
In fact, if you look up the compression strength of epoxy (the glue that’s usually used with carbon fiber), it’s ~10x weaker than dry carbon fiber. Meaning that, theoretically, a column of carbon fiber could withstand 10x more weight than a column of epoxy if those columns could somehow be made not to bend or buckle.
If the strength of the glue is not important, what is? What makes for a good glue? Well if you have a bundle of fibers where the glue doesn’t stick well, pushing on a single fiber will cause it to slip past its neighbors as they watch on helplessly -- like pulling a pin out of a pincushion. And if the glue isn’t stiff enough, the neighboring fibers might reluctantly support a little bit, but fibers further out won’t bother -- like half-done peanut brittle. When the sugary “glue” is fully set and hard, the whole batch of peanut brittle moves as a single unit. When the sugar stuff is hot and still malleable, you can pull away a peanut from the rest -- some might come with it, but for the most part, it’s every peanut for itself. So a good glue must stick strongly to the fibers and also have some stiffness of its own. This is what allows the glue to tie the fibers firmly together, so they can work as one unit.
To answer the opening question then: the compression capability that glue adds to fiber is why we don’t just make purely yarn-based airplanes. That added capability does not make the glued fiber a better material, just a different one. I think that’s a very important thing to note. The glued fiber opens up different design options than the unglued fiber. Aerospace engineering has evolved over time to favor monocoques. The fabric-covered, wood-framed planes of the past split duty between the fabric (made of unglued strands), which took only tension loads, and the wood frame, which took both tension and compression. In metallic or composite monocoques on the other hand, the skin takes both tension and compression. The idea is that this reduces or eliminates the need for a separate framework, potentially saving weight. In either case, a yarn on its own lacks stability, and needs external support -- by way of frame or glue -- to transcend from mere scarf to flying machine.
Corrections? Questions? Comments? I’d love to have your input. Leave a comment, email me at surjan@substack.com, or find me on LinkedIn.
Drawing exercise #14. If you missed it, here’s why I’m learning to draw.




