Imagining a Realistic Shelob
What would a giant spider look like in the real world?

Giant spiders are theoretically terrifying. In The Lord of the Rings, for instance, Shelob is shown to be stealthy and nimble despite her size. But would Shelob be so scary in reality?
I’ve been reading an interesting book called On Size and Life about the effect of scale on organisms, and the only thing I could think about was what Shelob’s legs would look like in real life. In our imaginations, giant spiders are just scaled up versions of the spiders we’re familiar with. But in order to function, the legs of a giant spider would have to be less spindly and more elephantine.
We can think of spider legs as columns under compression. Under compression, things usually break by buckling. Or, in other words, they break by becoming unstable -- think dry spaghetti. If you scale up the thickness of a column in proportion to its length, you end up with something very unstable. So the thickness (diameter) has to grow quicker than the length. The relationship ends up being:
This relationship can be seen in things like the proportions of bones.
And the proportions of trees.
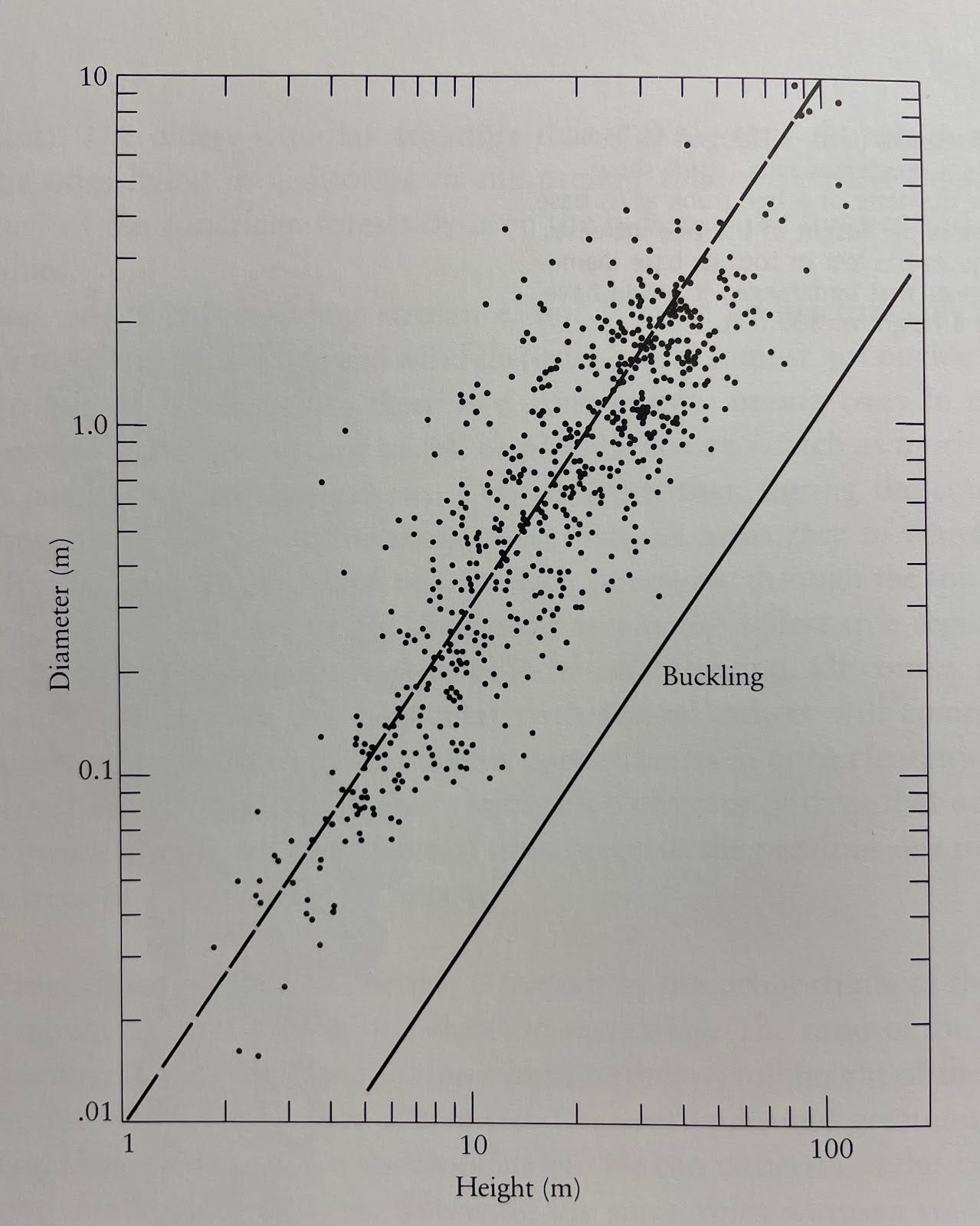
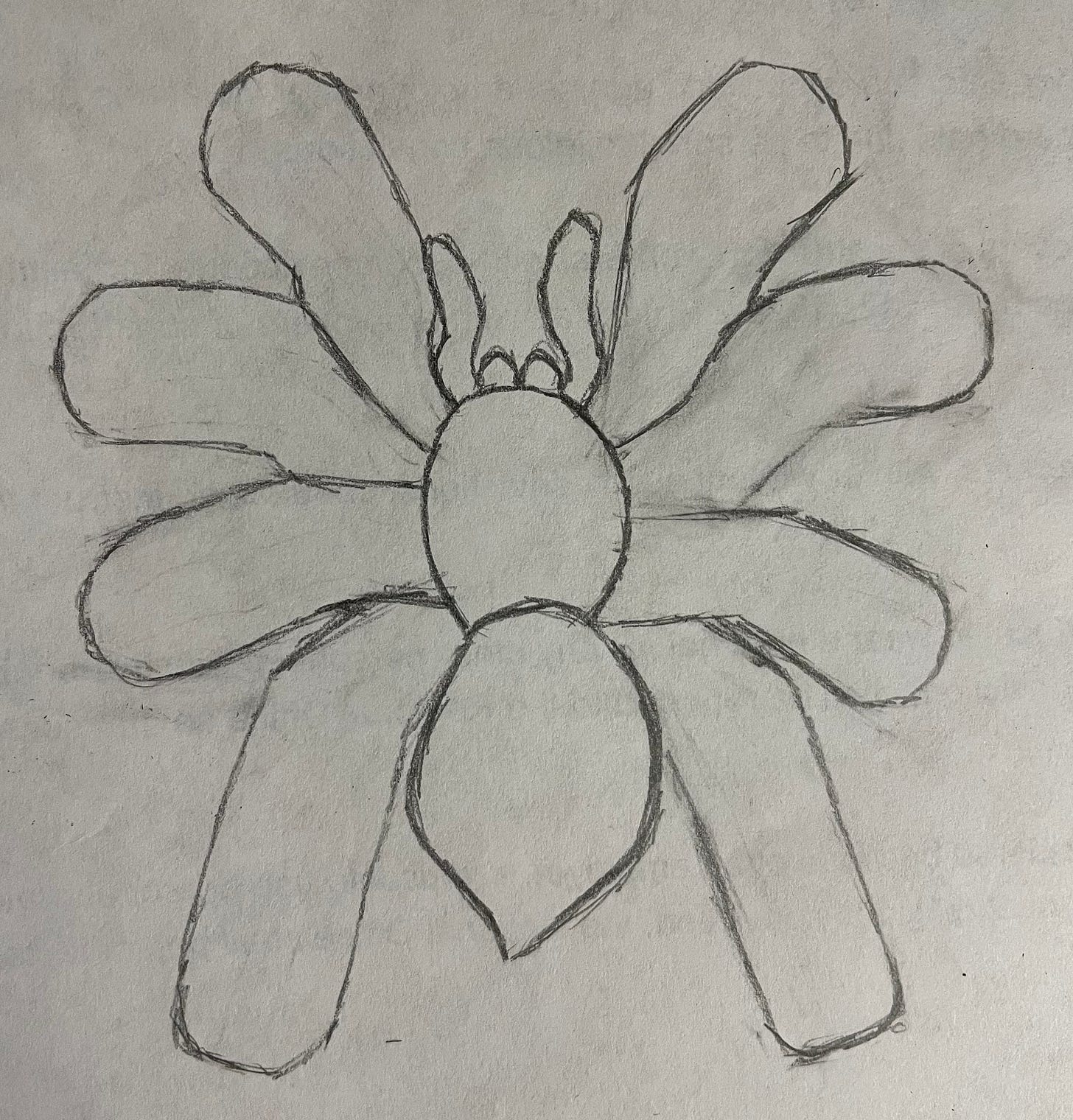
So what does that mean for Shelob? From Wikipedia, I know that a tarantula is about 4 inches long. From The Lord of the Rings wiki, Shelob is eight feet long, or 24 times longer than a tarantula. If Shelob’s legs are also 24 times longer than a tarantula’s, they would need to be 117 times thicker in order to avoid buckling. Or proportionally, about 5 times fatter than a tarantula’s leg. Here’s what that might look like.
Not quite as intimidating. Kinda looks like Fernando Botero’s fat animal sculptures.
How much would Shelob weigh? We’ll first estimate the volume roughly as the length cubed. So Shelob is 24³ ≈ 13,000 times more voluminous than a tarantula. I’m going to assume that the guts of a giant spider are the same as a normal one. In other words, the densities of the spiders are the same. So Shelob is 13,000 times heavier than a tarantula, which weighs roughly a third of a pound. Shelob weighs 13,000 * ⅓ lb ≈ 4000 lbs (1800 kg). That’s about the same as a rhinoceros.
What does that tell us about speed? Larger animals have a longer stride and should be faster, but they also expend more energy accelerating their bulk. So you could expect something a bit like a rhino, a short burst of speed up to 30 mph (50 kph), but not for a long time. And because of that mass, Shelob wouldn’t be able to stop on a dime or be very agile at all.
Shelob also wouldn’t be able to climb up walls. The surface of her feet increases as length squared, but the weight increases as length cubed. Shelob would be 13,000 times heavier but would only have 570 times more area in contact with the wall. In other words, the attraction between her feet and the wall would have to magically become about 20 times stronger.
So in reality, a giant spider would be a heavy, lumbering thing that would get winded after a short sprint, couldn’t climb walls, and probably couldn’t sneak up on you.
Shoutout to Kevin, whose estimation of how fast plants grow showed me how much I liked reading someone else’s back of the envelope calculations and convinced me to write this instead of just thinking it.
Also, in case you missed it, I recently wrote an issue for The Prepared.




I really like this! I remember watching a Bill Nye episode as a kid that covered this very topic. There was no math or technical discussion though, it was mostly just "insect or spider legs wouldn't be able to support their weight at that size". I do a fair bit of structural engineering professionally, but I never thought to actually do the math on this particular thing. I'm glad you did!